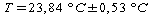Questa
esercitazione si pone come obiettivo quello di misurare la resistenza
elettrica della Pt100 e ricavarne la temperatura. Verrà poi
verificata l’incertezza a 0°C e a temperatura ambiente
tramite termometro di riferimento.
Si
stimerà l’effetto della resistenza dei cavi di
collegamento al sensore Pt100.
Materiale
utilizzato:
un
sensore PT100 con collegamento a 4 morsetti con cavo schermato
un
multimetro da banco con risoluzione di 6.5 cifre HP34401
resistori
bread-board
per circuiti elettrici
termometro
campione
thermos
con ghiaccio
Incertezze
nel circuito:
1)risoluzione
del multimetro:
Per
avere effetto della risoluzione trascurabile rispetto all'incertezza
del sensore Pt100, per esempio 0.01°C, si deve avere una
risoluzione nella misura della resistenza di circa 4 m
che equivale a dire che si necessita sulla portata 100
fondo scala, di una risoluzione
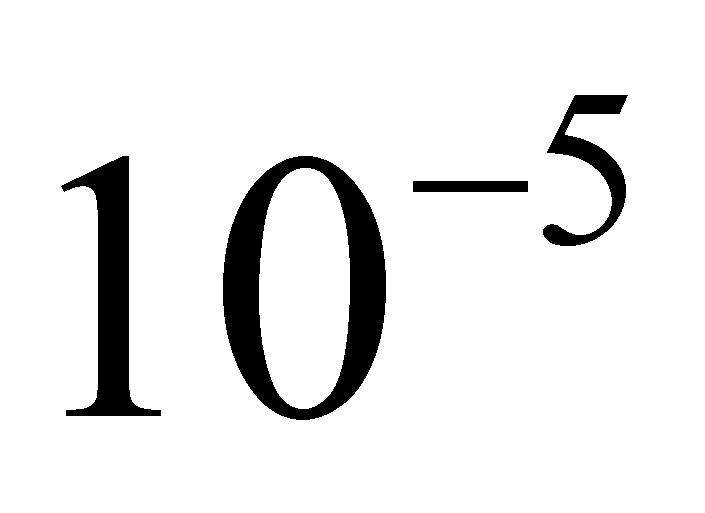 .
.
Noi
abbiamo impostato lo strumento per funzionare a 6.5 cifre quindi con
una risoluzione di 0,1 m.
2)resistenze
dei cavi di collegamento:
Le
resistenze di contatto per i dispositivi di connessione impiegati
possono essere di circa 0.02 ,
che equivalgono ad un errore di circa 0.05°C. Le resistenze dei
cavi, per un cavo da 0,5
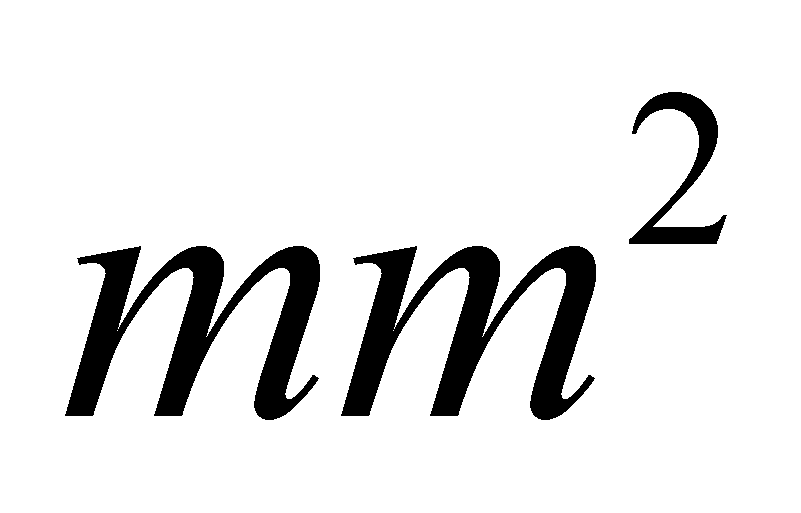 ,saranno
pari a circa 0,08 /m
che si traduce in un errore di 0.2°C/m.
,saranno
pari a circa 0,08 /m
che si traduce in un errore di 0.2°C/m.
Queste fonti di errore possono
essere eliminate impiegando una configurazione di collegamento del
Pt100 a 4 morsetti.
3)autoriscaldamento:
La
potenza dissipata dal sensore Pt100 è RI^2 e dipende dalla
corrente che scorre nel circuito e dalla resistenza della Pt100, che
però è fissa. La resistenza termica del sensore potrà
essere di circa 0.3°C/mW, quindi per esempio con una corrente di
1 mA , l’autoriscaldamento, per effetto joule, provocherà
un innalzamento della temperatura di circa 0.03°C non
trascurabile.
Risulta
evidente che conviene mantenere bassa la corrente nel sensore in modo
da limitare l’autoriscaldamento, ma non troppo, per non
compromettere l’accuratezza della misura.
Si
potrebbe pensare di misurare la resistenza termica del sensore e
correggere questo errore. Questo parametro è difficile da
misurare accuratamente. Di conseguenza trattiamo l’autoriscaldamento
come una fonte di incertezza.
4)FTEM:
Forze
Termo - Elettromotrici : si creano alla connessione platino-rame.
Possono
valere 10 – 100 uV. Sono all'incirca proporzionali alla
temperatura e causano
un’
incertezza che dipende dalla corrente con cui lavora il multimetro.
Il multimetro da noi utilizzato misura la resistenza come caduta di
tensione sul resistore quando percorso da una corrente di 1 mA (per
la portata 100 fondo
scala
fondo scala); perciò la tensione che viene misurata è
di 100 mV.
Le
FTEM possono pesare tra 10^-3 e 10^-4 cioè tra 0.01°C e
0.1°C.
Possiamo
eliminarle invertendo la tensione di alimentazione del circuito ed
eseguendo 2 misure.
Questo non risulta fattibile dal
momento in cui si utilizza il multimetro come misuratore di
resistenza.
5)presenza
di disturbi elettromagnetici nell’ambiente di misura:
Per
ridurre il problema si utilizzano cavi schermati per i collegamenti
la Pt100. I cavi hanno l'effetto di ridurre significativamente
l’influenza dei disturbi elettromagnetici che potrebbero
concatenarsi al segnale di misura.
Occorre,
inoltre, settare il tempo di integrazione del multimetro a 200 PLC
(200*20ms = 4 s).
Di
conseguenza la finestra temporale di integrazione si allarga, si
ottiene una reiezione ai disturbi a 50 Hz e, contemporaneamente, si
riduce l’influenza del rumore casuale gaussiano, poiché
integrato su un tempo più lungo. Nel circuito in figura sono
presenti diverse fonti di rumore : il rumore termico, dovuto alle
vibrazioni termiche dei materiali, il rumore shot dovuto ai
dispositivi attivi e il rumore 1/f o flicker.
6)incertezze
dovute al sensore:
Le
incertezze dei parametri di modello del sensore come A, B, C e R0
sono incognite.
Tuttavia,
è possibile fare alcune ipotesi ricorrendo ad un modello
deterministico della Pt100 e calcolarle.
7)incertezze
di linearizzazione:
La
variazione della resistenza del sensore Pt100, al variare della
temperatura, è lineare solo in prima approssimazione. In
realtà, il legame tra temperatura e resistenza è
espresso con un polinomio di ordine 9, il quale consente di
raggiungere scarti molto piccoli (dell’ordine di una decina di
m°C) . I coefficienti di tale polinomio dipendono dalla purezza
del platino che costituisce il sensore e dal metodo con il quale lo
stesso è stato ottenuto.
Noi
impieghiamo le formule di Callendar- Van Dusen
-per
temperature comprese tra -200°C e 0 °C
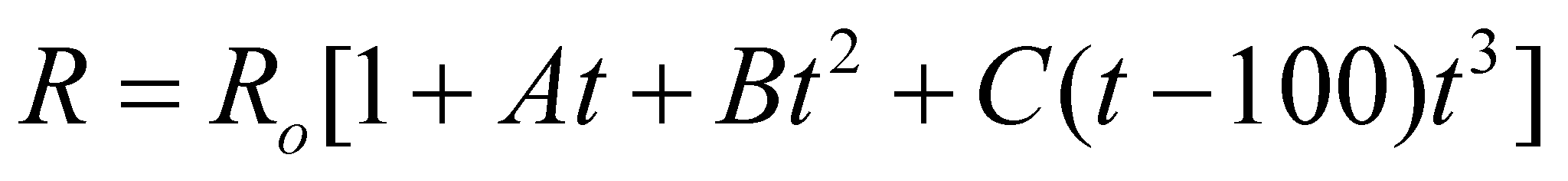
-per
temperature comprese tra 0°C e 850 °C 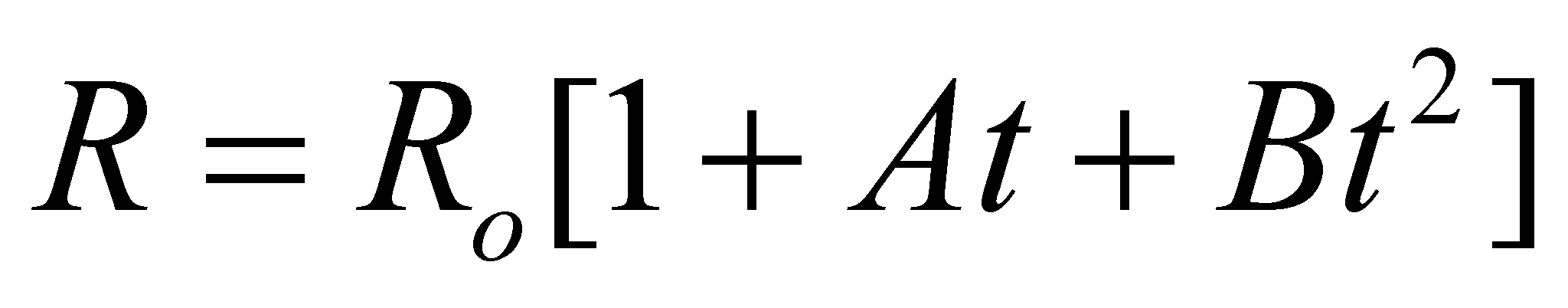
I
valori A, B, C dipendono dalla purezza del platino. Il nostro
sensore possiede un coefficiente
medio, tra 0°C e 100 °C, di 0.385%/°C.
Con
questo valore di
otteniamo:
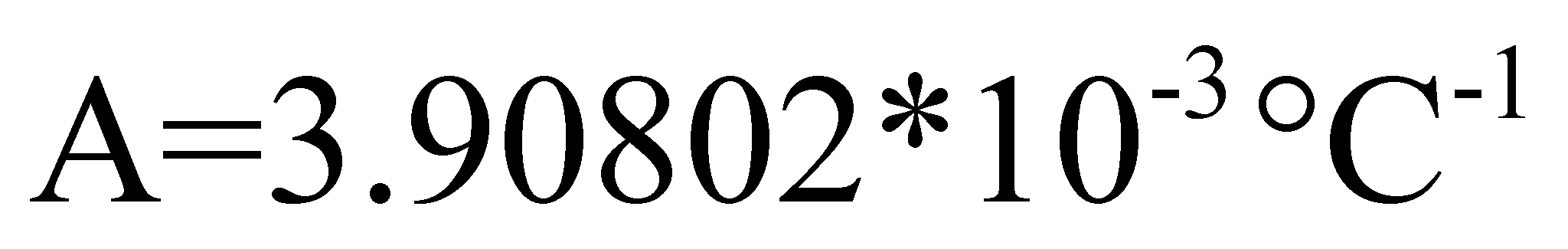
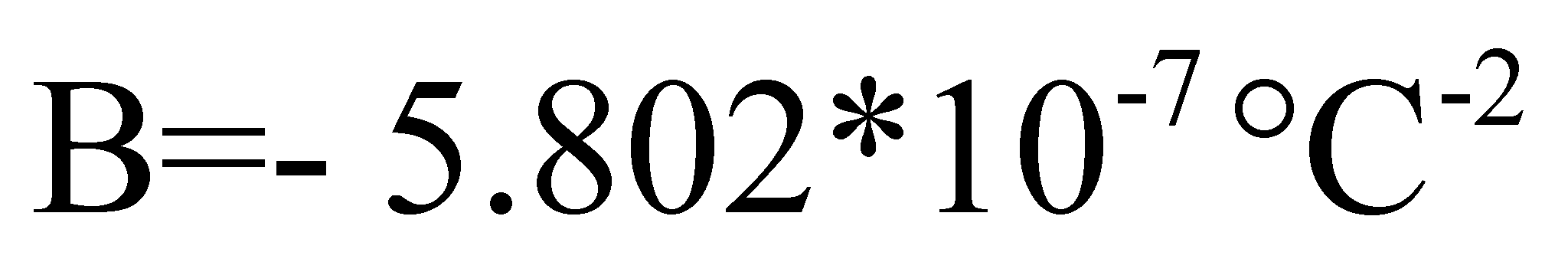
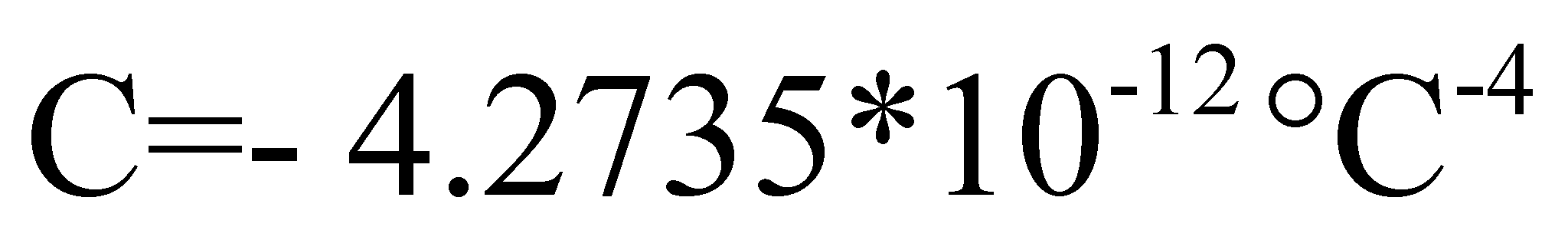
Impiegando
le formule di Callendar – Van Dusen commettiamo un piccolo
errore di linearizzazione del sensore. Si noti, inoltre, che il
valore assoluto dell’errore di linearizzazione cresce con
l’aumentare della temperatura.
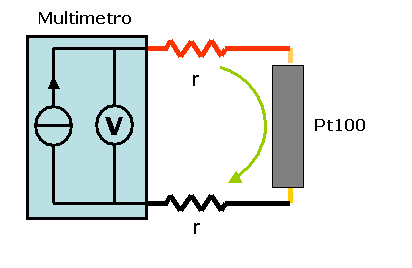
Figura
1 schema di collegamento a 2 morsetti
Procedimento:
Dopo aver assemblato lo schema in figura 1 e impostato il multimetro,
abbiamo misurato la resistenza del sensore PT100, impiegando la
configurazione a 2 morsetti.
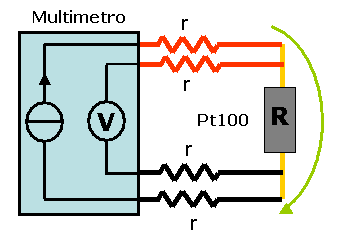
Figura 2
misurazione diretta con PT100 e DMM
Procedimento:
Dopo aver assemblato lo schema in figura 2 e impostato il
multimentro, abbiamo misurato la resistenza del sensore PT100,
impiegando la configurazione a 4 morsetti.
RISULTATI
-
La prima esperienza richiedeva di stimare la Resistenza
dei cavi (Rcavi
)
e valutarne
l’incertezza sulla misura. Ci siamo serviti di un multimetro HP
34401 a 6.5
cifre,in configurazione “Slow” in modo da avere una
misura più precisa.
Abbiamo
poi selezionato l’opzione 4 Wires che permette di misurare la
Rcavi
in modo preciso, tenendo anche conto dei conduttori usati per il
collegamento con il multimetro stesso.
Dal
multimetro abbiamo letto la seguente misura:
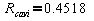 Ω
Ω
L’incertezza
della misura dipende dal multimetro, per cui dal manuale abbiamo
usato la seguente formula:

Avendo
usato un range di misura di 100 per effettuare la misura ricaviamo che:
per effettuare la misura ricaviamo che:
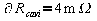
Quindi
la misura corretta è la seguente: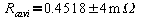
- Il
secondo punto dell'esperienza consisteva nel collegare la PT100 con
il multimetro ed effettuare la misura di resistenza con il sensore
immerso nel ghiaccio, in un primo momento, e poi a temperatura
ambiente.
Nel
primo caso con il sensore immerso nel ghiaccio abbiamo misurato un
valore di resistenza di pari a:
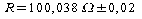
Per
trovare il valore della temperatura T ricorriamo alla formula di
Callendar-Van
Dusen:
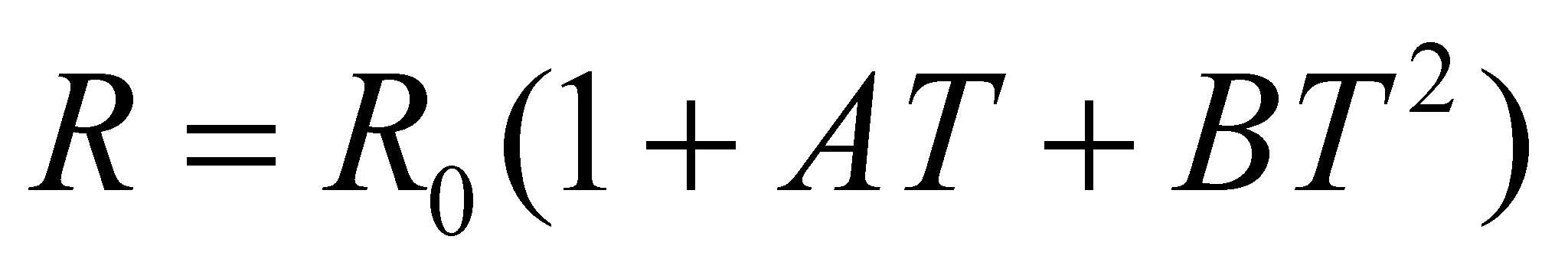
Invertendo
la formula, troviamo:
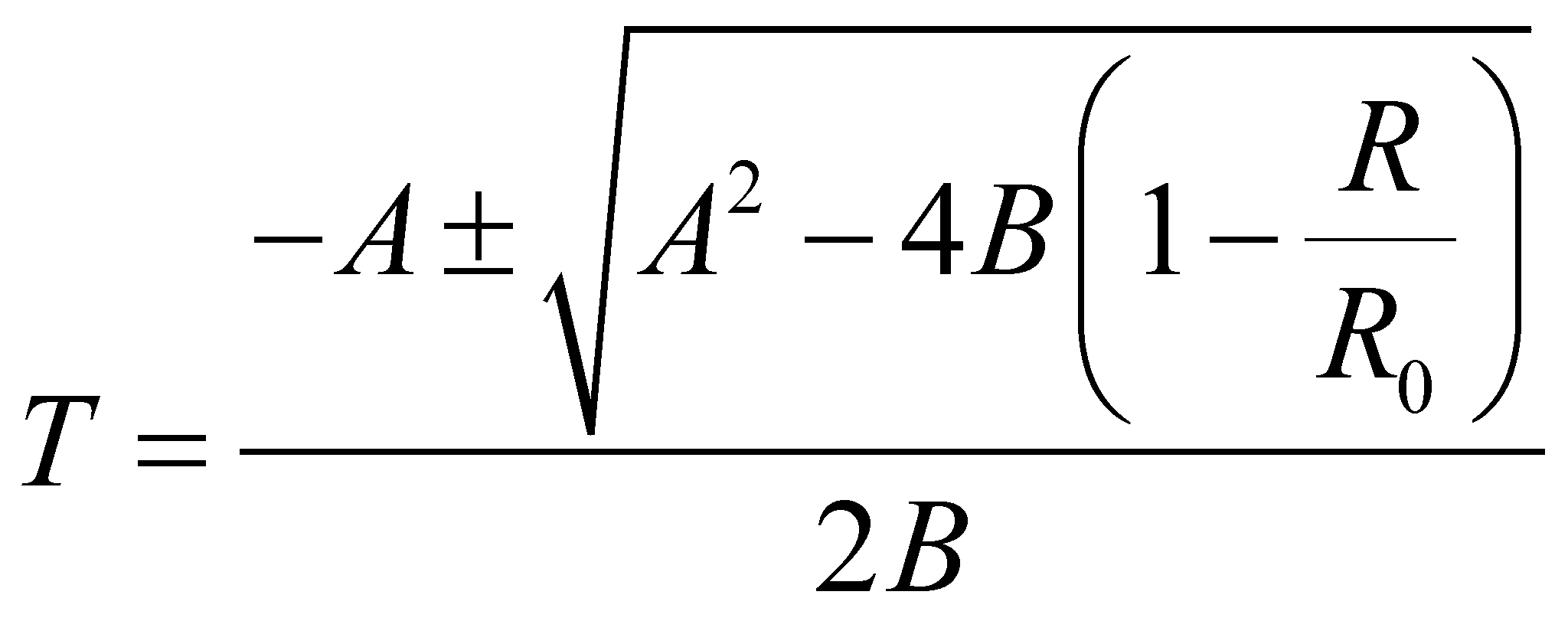
Dove
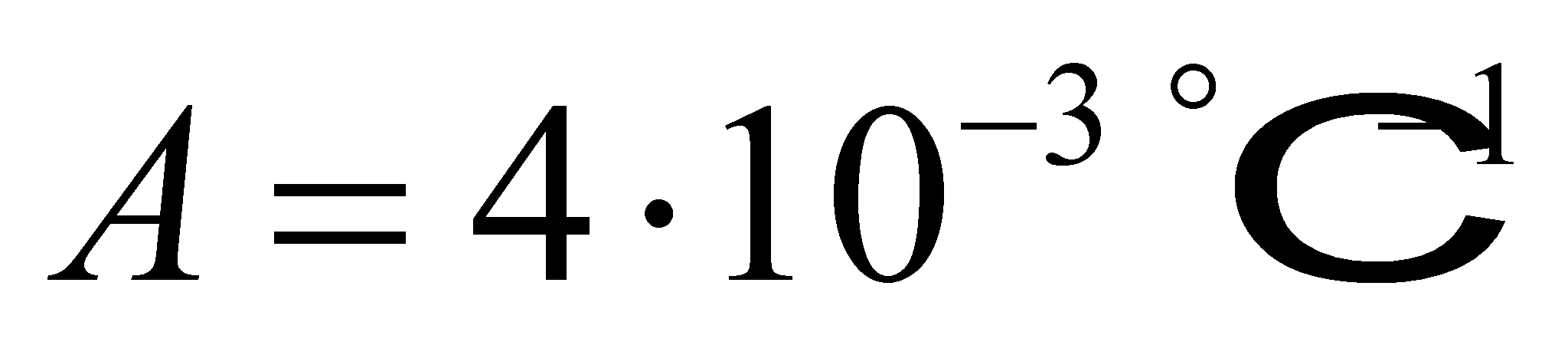 e
e
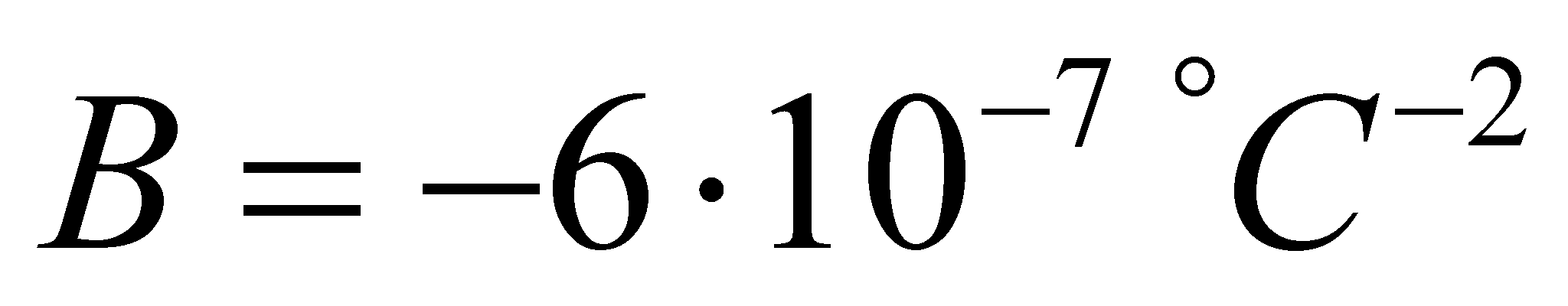 .
.
Troviamo,
quindi, due valori di temperatura:
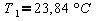
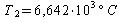
Come
si può facilmente osservare, la temperatura T2
non è reale; di conseguenza la temperatura corrispondente
alla R misurata è la T1.
INCERTEZZE:
1)Incertezze
del sensore:
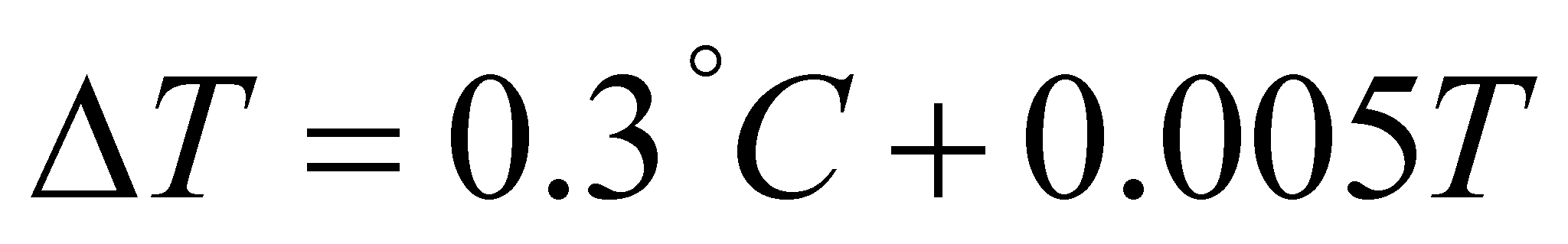
2)Incertezza
di misura:
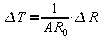
dove
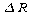 è
l'incertezza di misura della resistenza e
è
l'incertezza di misura della resistenza e
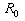 è
il valore della resistenza a 100°C.
è
il valore della resistenza a 100°C.
Otteniamo:
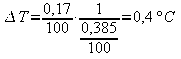
Per
tanto la misura corretta di temperatura sarà:
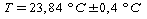
3)
Incertezze di modello
- FTEM:
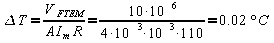
-linearizzazione
della Pt100:
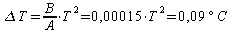
dove
T=25°C
-autoriscaldamento:
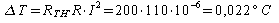
-non
consideriamo il contributo di incertezza dovuto ai cavi dal momento
in cui facciamo la misura a quattro morsetti
L'incertezza
totale vale :
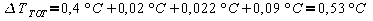
La
misura corretta é :