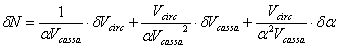Introduzione

Questa esperienza si prefigge di misurare la risposta in frequenza tra 50 Hz e 20 KHz di una cassa. La misura � relativa, in quanto, non disponendo in laboratorio di fonometri, non � possibile misurare il valore assoluto dell'intensit� sonora.

 

Materiale

- Resistori e condensatori vari

- Due amplificatori operazionali LF351

- Diodi 1N148

- Basetta per montaggi sperimentali (breadboard)

- Un alimentatore duale con tensione variabile -40V 0V + 40 V

- Due multimetri a 6.5 cifre HP 34401A

- Generatore di funzioni

- Microfono electret economico

 

I microfoni considerati

Abbiamo preso in considerazione due tecnologie costruttive: il microfono dinamico, e il microfono electret. Questi tipi di microfono sono infatti facilmente reperibili e economici in rapporto alla qualit�.

Il microfono dinamico sfrutta il fenomeno dell'induzione elettromagnetica per convertire le vibrazioni di una membrana in forza elettromotrice, grazie ad un avvolgimento di filo conduttore sottilissimo meccanicamente fissato alla membrana stessa. Tale struttura � immersa nel campo magnetico generato da un nucleo di magnete permanente. Il movimento della bobina mobile nel campo magnetico genera una corrente elettrica proporzionale all'ampiezza dei movimenti dell'avvolgimento e quindi all'ampiezza del segnale acustico.

Il microfono a condensatore, di cui l'electret ne � una variante, sfrutta invece un effetto capacitivo: � composto da due lamine che costituiscono un condensatore che varia la propria capacit� a causa delle vibrazioni prodotte dalle onde sonore. A differenza del microfono dinamico, dunque, questo tecnologia necessita di una alimentazione (detta "phantom power") per poter rilevare le variazioni di capacit� (o, considerando il concetto in altri termini, di una tensione per generare all'interno del condensatore il campo elettrico che sar� soggetto a variazione). Il microfono electret o elettrete � una variante del microfono a condensatore in cui si risolve tale inconveniente: dal momento che il condensatore � pre-polarizzato in maniera permanete al momento della costruzione, non necessita teoricamente di alimentazione. In realt�, data la debolezza del segnale generato, questi microfono hanno un piccolo circuto interno di amplificazione, che migliora i livelli di segnale, e adatta l'impedenza d'uscita del microfono per essere utilizzata con amplificatori di tensione con alta impedenza d'ingresso.

La risposta in frequenza dei due tipi di microfono � differente. Il microfono dinamico, essendo basato su un principio induttivo, ha scarsa sensibilit� alle basse frequenze, mentre ha ottime prestazione nelle frequenze medie. Salendo di frequenza, le dimensioni� della membrana diventano grandi rispetto alle lunghezze d'onda, perci� il microfono perde di sensibilit�.� Per questi motivi viene spesso utilizzato per la voce umana. Il microfono electret invece ha una risposta pi� costante, anche nel caso dispositivi di bassa qualit�, grazie al prinicipio realizzativo basato sulla variazione di capacit�.

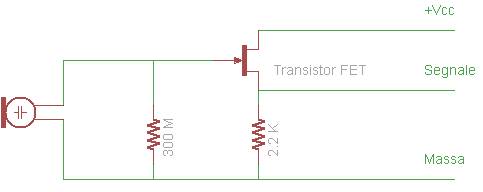
Poich� l'obiettivo dell'esperienza era la misura della risposta in frequenza, abbiamo scelto il microfono electret preamplificato, in modo da poter effettuare la misura in una banda ampia. Il microfono � un modello molto economico, con costo inferiore a 1 �,� presenta il circuito mostrato in figura, viene alimentato a +9V e fornisce in uscita una tensione continua alla quale � sommato il segnale, che ha ampiezze dell'ordine di 1mV.

 

 

 

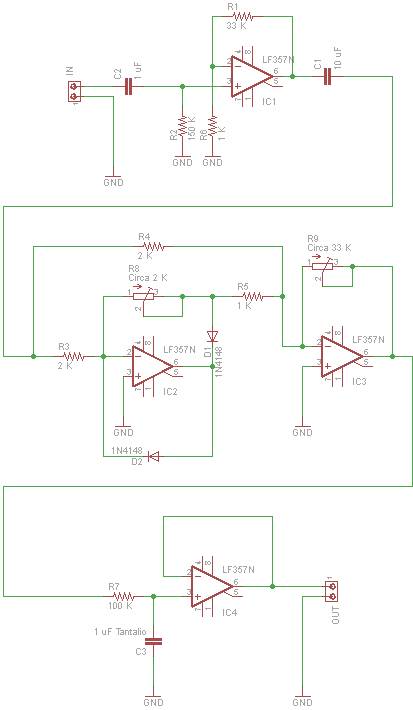
Il circuito

Il circuito pu� essere diviso in vari stadi, che possono essere presi in considerazione separatamente.

Il primo stadio � un filtro passa alto con lo scopo di eliminare la componente continua sommata al segnale del microfono. Poich� � collegato all'ingresso V⁺ di un amplificatore operazionale, la resistenza equivalente ai capi del condensatore coincide all'incirca con:

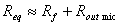
La resistenza di uscita del microfono � di difficile stima, in quanto richiede l'analisi del circuito interno. Si pu� stimare il suo valore come circa 50 - 100 Kohm, dato dalla somma della resistenza da 2,2 Kohm e dalla resistenza equivalente R_o del FET nel modello di piccolo segnale.

Sicuramente la frequenza di taglio del filtra sar� minore di:

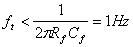
Tale valore � sicuramente accettabile per i nostri scopi, in quanto ci prefiggiamo di misurare la risposta in frequenza a partire da 50 Hz.

 

Eliminata la componente continua, il segnale deve essere ampificato. Poich� i livelli di uscita del microfono sono molto bassi (dell'ordine del mV) � necessario amplificare il segnale di circa 1000, ovvero 60dB. Tuttavia tale guadagno � eccessivo per uno stadio unico. Abbiamo perci� scelto di realizzare due stadi di amplificazione parziali, ciascuno con guadagno G_par = 30 = 30_db.

 

Lo stadio successivo al filtro � dunque un amplificatore non invertente:

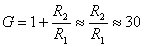
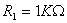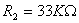E dunque �e . Facciamo notare che la scelta del guadagno e delle resistenze � approssimativa in questo stadio, perch� essendo la misura relativa, non importano i valori assoluti di tensione all'uscita del circuito, ma solo che abbiano valori accettabili.

 

All'usicita di questo stadio � presente un condensatore, con lo scopo di eliminare eventuali componenti continue dovute all'offset dell'operazionale. In caso contrario, la rettificazione dell'onda negli stadi successivi avverrebbe in modo errato. La resistenza equivalente ai capi di tale condensatore � costituita dal parallelo di R₃ e R₄ e dunque la frequenza di taglio del filtro � di circa 16 Hz.

 

I due stadi successivi costituiscono un raddrizzatore a doppia semionda di precisione. Date le tensioni in gioco (dopo l'amplificazione dello stadio 2, le tensioni sono dell'ordine delle decine di millivolt), non si possono trascurare le cadute di tensione e le non-linearit� che si avrebbero sui diodi di un ponte di Graetz. Il primo blocco � un raddrizzatore a singola semionda, che taglia la semionda negativa e riporta in uscita, invertendola, la semionda positiva. E' stato aggiunto un secondo diodo per evitare che, durante la semionda negativa, la tensione all'uscita dell'operazionale saturi a -Vcc improvvisamente, causando problemi dei slew rate.

Il secondo blocco � un sommatore che riceve in ingresso due segnali, e la cui tensione di uscita � data dalla formula:

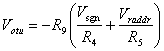
Il primo segnale � V_raddr, ovvero la singola semionda prodotta dal blocco precedente. Il secondo � V_sgn, ovvero il segnale originale, prelevato prima del raddrizzatore a singola semionda. V_sgn �

diviso per due impostando:

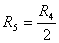
In questo modo, ipotizzando che il segnale originale sia simmetrico, come nel caso della sinusoide usata per la misura, la somma dei due segnali genera il segnale raddrizzato a doppia semionda, ovvero il modulo del segnale. Il sommatore completa l'amplificazione del segnale tramite 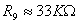, portando l'amplificazione complessiva .

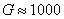Nel caso di segnale sinusoidale in ingresso, con frequenza f, il segnale all'uscita di tale raddrizzatore sar� dunque:

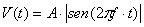
Con A>0 ampiezza del segnale.

 

Il circuito di media

La media del segnale all'uscita del raddrizzatore pu� essere calcolata partendo dalla definizione:

�

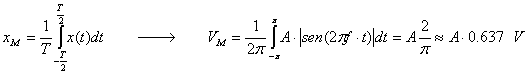Dove A>0 � l'ampiezza del segnale e T � il periodo.

 

Il circuito per calcolare la media � costituito da una resistenza e da un condensatore.

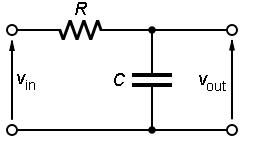
Consideriamo la legge di Kirchoff delle tensioni e la legge del condensatore:

�����������������������������

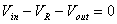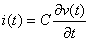
Otteniamo la tensione in uscita:

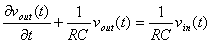
L'espressione � una equazione differenziale lineare del primo ordine, che ammette soluzione secondo la formula generica:

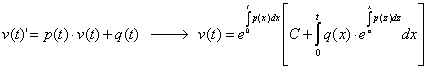
Dunque, nel caso del circuito, la soluzione sar�:

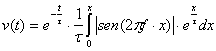
La soluzione esplicita di tale espressione � stata ottenuta mediate integrazione numerica con Matlab, o analitica con il pi� semplice Derive. In entrambi i casi, per un segnale con f=50hz e A=1V, si ottiene la soluzione seguente (tensioni in volt e tempo in secondi):

 

 

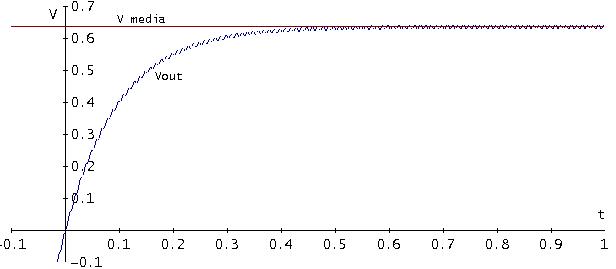
Come si vede dal grafico, all'inizio vi � un transitorio. In questo intervallo di tempo V_in>>V_out, e quindi V_out pu� essere semplificata nell'equazione differenziale esatta, ottenendo che:

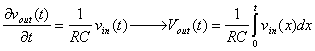
Il circuito si comporta cio� come un integratore ideale.

Esaurito il transitorio, si pu� notare come la tensione V_out tenda proprio al valore medio di V_in. Tuttavia permane un'ondulazione residua (detta comunemente ripple), che � maggiore alle basse frequenze, e decisamente minore alle alte frequenze. Questo comportamento pu� essere spiegato ricordando che alle basse frequenze il periodo dell'onda aumenta, avvicinandosi alla costante di carica e scarica 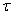�del condensatore.

 

Calcolo dell'incertezza sul circuito di media

Poich� il voltmetro misura la tensione V_out con intervalli sicuramente non uguali e in fase con il periodo T del ripple, dobbiamo considerare tale ondulazione come fonte di incertezza.

Per stimare l'incertezza introdotta, ci poniamo nel caso peggiore: frequenza pari a quella minima di 50Hz, ampiezza pari a quella massima misurata, ovvero circa:

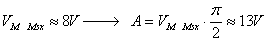
Risolviamo numericamente l'integrale in un intervallo di tempo in cui si pu� supporre di essere in condizioni di regime, ad esempio tra 3 e 4 secondi. Individuiamo poi l'incertezza come la massima distanza tra il valor medio esatto 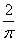�del segnale, e la tensione V_out.

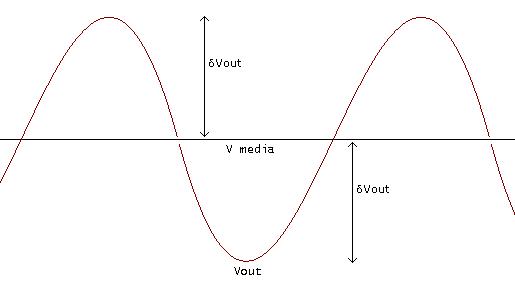
Si ottiene che tale distanza � di circa 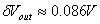. La tensione misurata avr� dunque una incertezza relativa:

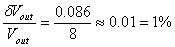
Bisogna tuttavia ricordare che i voltmetri digitali impiegati non campionano la tensione esattamente in un istante (come si � supposto nei calcoli precedenti), ma effettuano la misura in un intervallo di tempo. Pi� l'intervallo di misura � lungo, pi� il peso delle variazioni di tensione nella misura finale si attenua. Tuttavia, una stima dell'incertezza dovuta al ripple che tenga conto anche dei circuiti del voltmetro risulta troppo complicata per i fini di questa relazione. Possiamo assumere il valore di 1% come stima dell'incertezza massima, o equivalentemente, come limite superiore.

 

Il dimensionamento del circuito di media

Per il dimensionamento dei componenti del circuito si possono fare le seguenti considerazioni. Affinch� la tensione V_out sia quasi costante, � necessario che la costante di scarica e carica 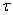�del condensatore sia molto pi� grande del periodo della tensione sinusoidale V_in all'ingresso del circuito.

La costante di tempo pu� essere calcolata considerando che la resistenza equivalente ai capi del condensatore � circa R₇, in quanto prima del blocco c'� l'uscita di un operazionale, che pu� essere approssimata a un cortocircuito in serie a R₇, mentre dopo il blocco c'� l'ingresso di un operazionale, che pu� essere approssimato come un circuito aperto in parallelo a R₇. Scegliendo 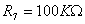�e 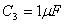�si ottiene 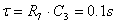. Il periodo pi� grande si avr� alla frequenza di misura minore, cio� f_min=50Hz :

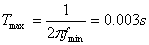
Dunque la costante di tempo del filtro 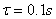�� pi� che sufficiente per ottenere valori di tensione pressoch� costanti e proporzionali al valore medio del segnale, e dunque a quello efficace, nel caso di segnali sinusoidali. Il condensatore � stato scelto al tantalio per l'elevata qualit� che questa tecnologia offre.

 

La scelta dei diodi

Abbiamo preso in considerazione i diodi disponibili in laboratorio: 1N4007, molto comune e utilizzato come diodo per usi generici, e 1N4148, utilizzato principalmente per applicazioni switching. Non dovendo trattare con tensioni o correnti di elevati valori, il fattore determinante per la scelta del diodo � stato la capacit� parassita. Alla frequenza di 1 Mhz, con V_inversa = 4 V, per 1N4007 questa � di 15pf, mentre per 1N4148 � di 1pf. Abbiamo dunque scelto 1N4148.

Tenere conto di tale capacit� parassita in fase di progetto � piuttosto complicato. Abbiamo perci� scelto di misurare a posteriori la risposta in frequenza del circuito per tenere in considerazione tali problemi.

 

La scelta degli operazionali

Abbiamo preso in considerazione tre tipi di operazionale: OP07, LF351, LM358.

 

	OP07	LM358	LF351
Slew Rate [V/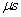]	0.17	0.6	16
Corrente di Offset [nA]	0.8	2	0.1
Tensione di Offset [mV]	0.06	2	10
Corrente di Bias [nA]	1.8	20	200
Prodotto banda-guadagno [Mhz]	0.5	1.1	4

 

Come risulta evidente dalla tabella, l'OP07 � volto all'utilizzo in bassa frequenza, mentre l'LF351 in alta frequenza. L'LM358 risulta un compromesso tra i due modelli, e infatti viene spesso utilizzato per scopi generali. Poich� nella nostra esperienza � essenziale che la risposta in frequenza del circuito sia il pi� regolare possibile, abbiamo scelto l'LF351.

 

La cassa misurata

Abbiamo scelto di misurare la risposta in frequenza relativa di una cassa di media qualit�: Bowers & Wilkins DM303. La cassa ha le seguenti caratteristiche:

 

Descrizione: diffusore a 2 vie con bass reflex con uscita posteriore

Frequenza (a -6dB): 52Hz - 30KHz

Potenza: 100W con impedenza 8 Ohm

Sensibilit�: 88dB spl ( con 2.83V a 1 metro)

Impedenza: media 8 ohm, minima 4.3 ohm

Dimensioni: 33.1 x 20.1 x 24.2 cm

Peso: 5 Kg

 

Principali fonti di errore

Abbiamo analizzato la catena di misura, e analizzato per ciascuno stadio le possibili fonti di errore e incertezza, e le possibili correzioni.

 

1) Risonanze e riflessioni della stanza: le onde sonore prodotte dal diffusore si riflettono contro le pareti della stanza e degli oggetti al suo interno, e per alcune frequenze entrano in risonanza. Questi due fenomeni alterano la misura della risposta in frequenza della cassa, perch� modificano l'ampiezza del segnale sonoro captato dal microfono.

Abbiamo provato a effettuare una stima delle possibili frequenze di risonanza della stanza, approssimandola a una cavit� rettangolare completamente vuota. Abbiamo misurato le dimensioni della stanza utilizzando un metro da muratore, spostandolo pi� volte dentro la stanza per coprire per intero ciascuna lunghezza. Considerando il metodo di esecuzione della misura, possiamo assumere una incertezza di circa 10cm per ogni dimensione della stanza. I valori sono:

 

Larghezza a: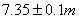

Lunghezza b: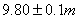

Altezza c: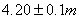

 

Abbiamo stimato le frequenze di risonanza con la formula:

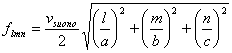
Riportiamo alcune frequenze di risonanza per i primi modi, a partire da 50Hz:

 

 

Come si pu� notare, le frequenze di risonanza della stanza sono molto vicine. Bisogna ricordare inoltre che la stanza non � vuota, ma contiene persone, mobili e oggetti, che possono sensibilmente modificare i valori calcolati.

Abbiamo perci� scelto di tenere conto di riflessioni e risonanze compiendo pi� misure, in posizioni diverse della stanza. Confrontando le differenze tra le varie risposte in frequenza sar� possibile individuare quali tratti della curva sono dovuti alla cassa e quali all'ambiente.

 

2) Generatore di funzioni: pu� generare tensioni tra 0 e 30 V, e ha una impedenza interna di 50 Ohm. Le incertezze dovute alla tensione errata o alla resistenza dei cavi � trascurabile, in quanto la tensione effettiva presente ai capi della cassa � stata misurata direttamente tramite uno dei due multimetri. La misura della tensione ai capi della cassa si rende necessaria anche perch� la sua impedenza � incognita. Abbiamo assunto che l'incertezza sulla frequenza sia trascurabile rispetto alla tipologia di misura.

 

3) Diffusore: � possibile che l'impedenza della cassa vari al cambiare della sua posizione all'interno della stanza, perch� le riflessioni e le risonanze del suono si accoppiano in modo differente con i coni. Abbiamo perci� scelto di misurare la tensione ai capi della cassa per ogni serie di misura per correggere tale errore.

 

4) Microfono: in tutta la catena, tale elemento � la fonte maggiore di errore e incertezza. Poich� non � nota la sua risposta in frequenza, possiamo solo supporre che questa, grazie alla tecnologia costruttiva adottata, sia piatta nella gamma di frequenze che ci interessa misurare.

 

5) Taratura del circuito: a causa delle capacit� parassite dei diodi e degli operazionali, la risposta del circuito non � piatta nella gamma di frequenze prese in esame. Abbiamo scelto di correggere tale errore misurando direttamente tale risposta in frequenza. Abbiamo posto all'ingresso del circuito una tensione sinusoidale generata dal generatore di funzioni, e abbiamo misurato l'uscita del circuito. Effettuando il rapporto:

��������������������������

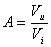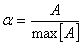
abbiamo ottenuto una serie di coefficienti A, che, normalizzati al loro valore massimo, rappresentano la risposta in frequenza del circuito, e verranno utilizzati per pesare opportunamente le misure.

La tensione V_i � stata ottenuta collegando il generatore di funzioni ai capi di un partitore resistivo, e prelevando la tensione ai capi di una resistenza, poich� lo strumento non era in grado di fornire tensioni cos� piccole. Poich� l'ingresso di un operazionale ha alta impedenza, indipendente dalla frequenza, possiamo supporre V_i costante e indipendente dalla frequenza. Poich� la misura � relativa, il valore esatto del partitore resistivo non � importante, e possiamo supporre un rapporto di partizione di circa 500, in modo da ottenere 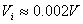�se V_generatore=1 V.

Calcoliamo dunque l'espressione esplicita dei coefficienti :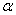

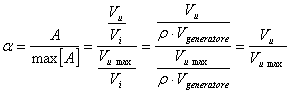
L'incertezza relativa non sar� costante per tutti i valori, perch� il voltmetro cambia fondoscala nella misura dei coefficienti. Consideriamo il caso peggiore:

�����

 

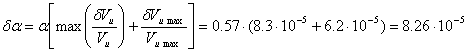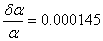
6) Inesattezza della media: abbiamo gi� discusso e stimato l'incertezza che il circuito introduce nel calcolo della media, ottenendo valori massimi dell' 1%.

 

7) Multimetro: abbiamo utilizzato i due multimetri per misurare la tensione ai capi della cassa (misura in AC) e all'uscita del circuito (misura in DC). Il multimetro presenta i seguenti valori di incertezza:

 

- Tensione continua, fondoscala 100mV: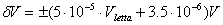

- Tensione continua, fondoscala 1V: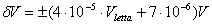

- Tensione continua, fondoscala 10V: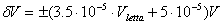

 

- Tensione RMS, 10 Hz - 20Khz, fondoscala 100mV: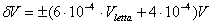

- Tensione RMS, 10 Hz - 20Khz, fondoscala 750V: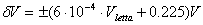

 

Risposta in frequenza della cassa

Per ciascuna serie di misure, sono state prese le seguenti misure:

- Tensione efficace ai capi della cassa

- Tensione continua all'uscita del cicuito

 

Per trovare la risposta in frequenza relativa � stato effettuato il rapporto N tra le tensioni di uscita e ingresso al sistema, pesato con la risposta in frequenza del circuito normalizzata. Tali valori sono poi normalizzati al valore massimo (coefficienti 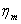) o al valor quadratico medio (coefficienti )

��������������� ����������������������������������

 

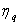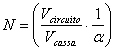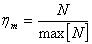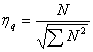
Incertezza

Abbiamo scelto di stimare l'incertezza nel caso peggiore, e di utilizzare tale valore per tutte le misure. Possiamo stimare l'incertezza di un coefficiente come:

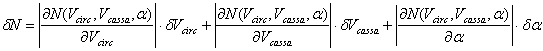
Ovvero: